Today I will implement another important abstract data type – priority queue. Priority queues are used:

• in heap sort
• to track top N elements in a very long sequence
• to merge K ordered sequences and produce single ordered sequence

Usually priority queues have following functions:

• insert() – to add new item with a priority
• deleteMin() or deleteMax() – to remove an item with min/max priority
• findMin() or findMax() – to get an item with min/max priority
• length() – to get the number of items in the priority queue

As a foundation I’ll use in the last post described efficient data structure – binary heap (in fact, max-heap). Overall, priority queue can be seen as a generalization of stack and queue data structures. Stack can be implemented as a max priority queue where priority of each inserted element is monotonically increasing and queue – where priority of each inserted element is monotonically decreasing.

The implementation of max priority queue (tests) is almost identical to the max-heap implementation:

Complexity:

• insert - O(logn)
• deleteMin/deleteMax - O(logn)
• findMin/findMax - O(1)

Today I will implement very efficient data structure – binary heap. Binary heap – is an array-based complete binary tree (binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible) which satisfies one of the following ordering properties:

• min-heap – the value of each node is not smaller than value of its parent with smallest element at the root;
• max-heap – the value of each node is not bigger than value of its parent with biggest element at the root Binary heap is a foundation for an abstract data type - priority queue, wich I will cover in next post.

Due to the nature of binary heap (complete binary tree) it can be very efficiently implemented using dynamic array. Items in the array are usually stored starting from index 1, thus allowing very easy navigation through binary heap:

• for the item with index k its parent index is k >> 1
• for the item with index k children indexes are k << 1 and k << 1 + 1

Usually binary heaps have following functions:

• insert() – to add new item
• delete() – to remove min or max item (depending on the ordering)
• length() – to get the number of items in binary heap

To add new item:

• add the item to the bottom level of the binary heap (as the last possible item)
• compare added item with its parent
• if they are in correct order – break
• else – exchange items and repeat with the parent

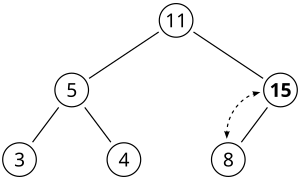
To delete maximum item (for max-heap) or minimum item (for min-heap):

• replace the root of the binary heap with the last item on the bottom level
• compare new root with the biggest (for max-heap) or  smallest (for min-heap) of children
• if they are in correct order – break
• else – exchange items and repeat with the selected child

Bellow you can find possible implementation of the binary heap (tests):

Complexity:

• insert - O(logn)
• delete - O(logn)

Recently at Build Stuff conference I gave a practical talk on Continuous Delivery. Enjoy and tell what you think!